Zadania z szybkości
1.Julek ma trening o siedemnastej. O której godzinie najpóźniej musi wyjść z domu, aby dotrzeć na miejsce 15 minut przed treningiem, jeżeli ma do przebycia 14 km. Średnia szybkość z którą jedzie autobus o tej porze dnia wynosi 35 km/h.
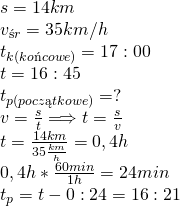
2.Gośka i Ewa umówiły się na godzinę piętnastą na rowery w parku. Gośka kończy swoje zajęcia o 14.15, a Ewa 20 minut później. Z jaką minimalną średnią szybkością musiałaby jechać na rowerze każda z nich, żeby zdążyć, jeżeli Gośka ma do przebycia odległość 7 km, a Ewka 3 km.
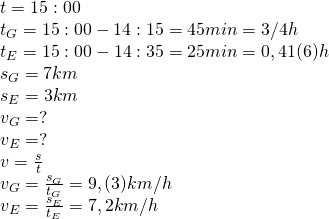
3.W czasie pierwszych 30 minut kierowca jedzie autostradą z Krakowa do Chrzanowa ze średnią szybkością 95 km/h. Następnie zjeżdża z autostrady i przez kolejne 45 minut porusza się ze średnią szybkością 45 km/h. Oblicz średnią szybkość kierowcy na całej trasie.

4.Rowerzysta przez półtorej godziny treningu jedzie ze średnią szybkością 12 m/s, a kolejne 6 km przebywa w czasie 10 minut. Oblicz średnią szybkość rowerzysty w czasie całego treningu.
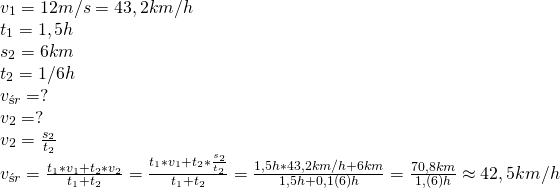
5.Pierwsze cztery okrążenia o długośći 400 m każde lekkoatleta przebiega w czasie 4 min i 20 sekund, kolejne trzy i pół okrążenia w czasie 6 minut, a ostatnie 200 m przebiega z szybkością 8 m/s. Oblicz średnią szybkość lekkoatlety.
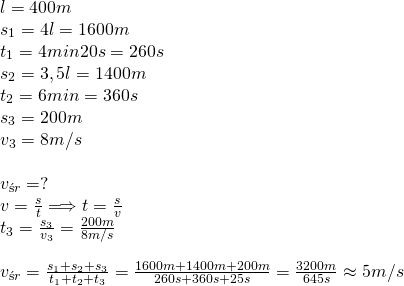
6.Elka codziennie biega. Oblicz jej średnią szybkość, wiedząć, że pierwszą połowę drogi przebiega z szybkością 2,4 m/s, a drugą połowę z szybkością 1,2 m/s.
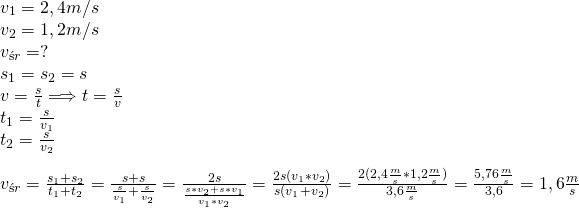
7.Oblicz średnią szybkość kierowcy na trasie Kraków-Sandomierz, wiedząć, że przez pierwszą połowę czasu poruszał się on ze średnią szybkością 50 km/h, a przez drugą połowę ze średnią szybkością 80 km/h.
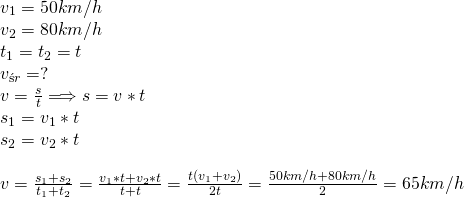
8.Pierwszą połowę drogi z Krakowa do Krościenka bus przebywa ze średnią szybkością 30 km/h, drugą połowę ze średnią szybkością 60 km/h. W drodze powrotnej przeez pierwszą połowę czasu porusza się ze średnią szybkością 80 km/h, a przez drugą połowę czasu, ze średnią szybkością 60 km/h. Oblicz średnie szybkości busa na trasach:
a) z Krakowa do Krościenka
b) z Krościenka do Krakowa
c) z Krakowa do Krościenka i z powrotem

9.Średnia szybkość motocyklisty na całej drodze była równa 30 m/s. Jeżeli 1/3 drogi przebył z szybkością 2 razy większą niż pozostałe 2/3 drogi, to z jaką szybkością średnią przebył każdy z tych odcinków?
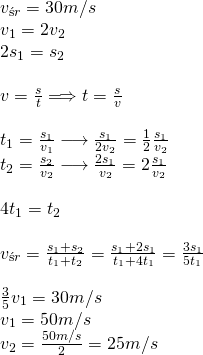
10.Motocyklista całą trasę przebył się ze średnią szybkością 90 km/h. Oblicz, z jaką średnią szybkością poruszał się w pierwszej połowie czasu ruchu, jeżeli jego średnia szybkość była wówczas trzy razy mniejsza niż w drugiej połowie czasu.
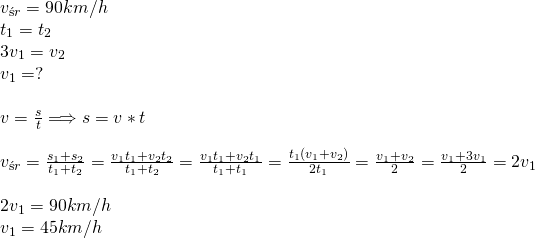
11.Marysia wyszła z domu do sklepu oddalonego o 300m. W sklepie zorientowała się, że nie wzięła portfela, więc musiała wrócić do domu. Oblicz średnią szybkości wartość średniej prędkości dziewczynki, jeżeli od jej wyjścia z domu do jej powrotu minęło 10 minut.
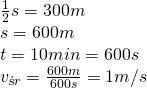
12.Dla młodzieży przygotowano tor gokartowy w kształcie okręgu o promieniu 12 m. Oblicz:
a) średnią szybkość i wartość średniej prędkości zawodnika, który przebył dziesięć pełnych okrążeń w czsie 75,36 s;
b) wartość średniej prędkości zawodnika po czasie odpowiednio równym: 1/4 okresu (czyli czasu, w którym zawodnik wykonuje jedno pełne okrążenie), 1/2 okresu, 1/6 okresu.
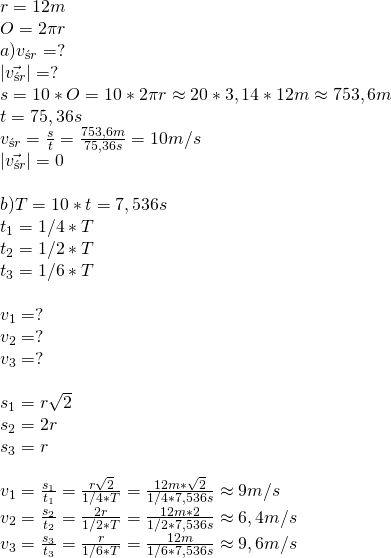
15. Pies przebiegł po trawniku z punktu ![]() do punktu
do punktu ![]() w czasie 14 sekund. Tor jego ruchu przedstawia odcinek
w czasie 14 sekund. Tor jego ruchu przedstawia odcinek ![]() na wykresie
na wykresie ![]() .
.
a) Rozstrzygnij, czy na podstawie wykresu można wyciągnąć wniosek jakim rodzajem ruchu poruszał się pies.
b) Oblicz drogę przebytą przez psa.
Mając dodatkową informację, że ruch psa był ruchem jednostajnym, oblicz:
c) jego szybkość,
d) współrzędne ![]() i
i ![]() jego prędkości.
jego prędkości.
![]()
a) Nie można, ponieważ mógł on przyspieszać, zwalniać, zatrzymywać się, itp. Wiemy jedynie, że poruszał się ruchem prostoliniowym.
b)
![]()
c)
![]()
d) korzystamy z tw. Talesa
![]()
![]()
![]()
(wektor skierowany jest w dół osi)
![]()
18.Młoda foka, widząc orkę w odległości 50 m za sobą, zaczyna uciekać z szybkością 43,2 ![]() . Orka płynie w jej kierunku z szybkością 50,4
. Orka płynie w jej kierunku z szybkością 50,4 ![]() . Napisz równania ruchu foki i orki, przyjmując, że dla orki
. Napisz równania ruchu foki i orki, przyjmując, że dla orki ![]() . Następnie wykonaj polecenia:
. Następnie wykonaj polecenia:
a) Oblicz czas, po którym orka dogoni fokę.
b) Oblicz współrzędną miejsca spotkania zwierząt
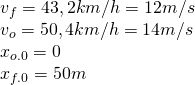
ogólne równanie ruchu dla ruchu jednostajnego prostoliniowego to
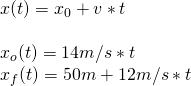
a)
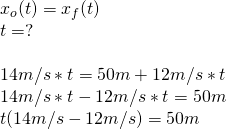
![]()
b)
![]()
.
20.Dwaj kajakarze poruszają się wzdłuż tej samej prostej. Pierwszy zaczyna ruch z miejsca oznaczonego napisem START i płynie przez pierwsze 25 sekund z szybkością 3 ![]() , a następnie z szybkością 2
, a następnie z szybkością 2 ![]() . Drugi kajakarz płynie z szybkością 3,5
. Drugi kajakarz płynie z szybkością 3,5 ![]() , ale wyrusza z miejsca położonego 15 metrów za tym puunktem i o 16 sekund później od chwili startu pierwszego sportowca. Oblicz, kiedy i gdzdie, licząc od punktu startu, zawodnicy się spotkają.
, ale wyrusza z miejsca położonego 15 metrów za tym puunktem i o 16 sekund później od chwili startu pierwszego sportowca. Oblicz, kiedy i gdzdie, licząc od punktu startu, zawodnicy się spotkają.
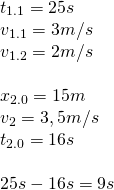
gdy pierwszy jest w 25 sekundzie ruchu, drugi jest w 9s
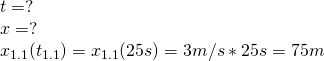
![]()
W t=25s od chwili startu zawodnika 1 znajduje się on w położeniu ![]() , a zawodnik 2 będzie w
, a zawodnik 2 będzie w ![]() .
.
![]()
Można to dla ułatwienia liczyć jako drugi start obu z nich. Wówczas równania ruchu dla obu z nich wyglądają następująco:
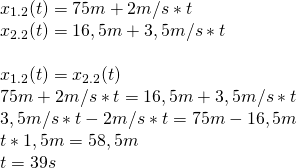
Ostateczny czas to 25s+39s=64s od startu pierwszego zawodnika.
![]()
b)
![]()
21. Gepard, poruszając się ruchem jednostajnie przyspieszonym z szybkością początkową równą zeru, w czasie 12 sekund przebywa drogę 216 m. Oblicz wartość przyspieszenia geparda i szybkość, którą osiągnie po tym czasie. Wyraź szybkość w km/h.
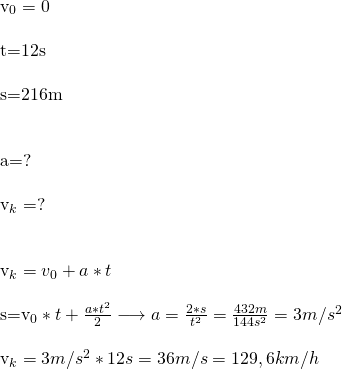
22. Samocód ciężarowy porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem o wartości 0,8 ![]() . Oblicz, po jakim czasie samochód osiągnie szybkość 64,8
. Oblicz, po jakim czasie samochód osiągnie szybkość 64,8 ![]() oraz drogę, którą przebędzie w tym czasie, jeżeli prędkość początkowa wynosi zero.
oraz drogę, którą przebędzie w tym czasie, jeżeli prędkość początkowa wynosi zero.
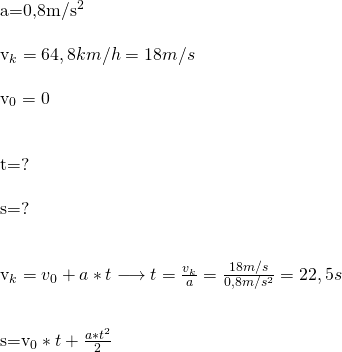
![]()

 (251 votes, average: 4,31 out of 5)
(251 votes, average: 4,31 out of 5)