permalink

Modelowanie rozprzestrzeniania się epidemii

Wstęp

Od pewnego czasu temat modelowania epidemii staje się coraz popularniejszą i dynamicznie rozwijającą się dziedziną badań naukowych. Dzięki postępom poczynionym w tej sferze nauki, jesteśmy dzisiaj w stanie przewidywać do pewnego stopnia scenariusze i skomplikowaną dynamikę rozprzestrzeniania się infekcji w populacjach. Pozwala to na skuteczne dopasowywanie odpowiednich strategii wdrażanych jako środki prewencyjne oraz zaradcze, gdy do epidemii już dochodzi, takich jak kwarantanny, izolacja, szczepienia, badania przesiewowe, czy dystrybucja leków.
Charakter sieci społecznych mocno sprzyja rozprzestrzenianiu się wirusów, przez co walka z chorobami zakaźnymi potrafi być ogromnie trudna. Nie mniej jednak, za pomocą numerycznego modelowania po raz pierwszy jesteśmy w stanie w jakimś stopniu kontrolować epidemię i wpływać na jej przebieg, a na pewno wdrażać jak najbardziej skuteczne strategie.

Sieć definiuje się najprościej jako zbiór wierzchołków lub inaczej węzłów, połączonych krawędziami. Przez węzły rozumie się reprezentację pewnych obiektów, a przez krawędzie relacje między nimi. W przypadku analizowania przebiegu epidemii chcemy opisać sieć społeczną, a dokładnie sieć kontaktów międzyludzkich, więc węzły sieci symbolizują konkretne osoby, a krawędź między węzłami oznacza, że dane dwie osoby mają ze sobą kontakt.

Poniżej zostaną przedstawione dwa podstawowe modele epidemiologiczne wdrażane na sieciach typu klasyczny graf przypadkowy oraz na sieci bezskalowej, która znacznie lepiej przybliża charakterystykę rzeczywistych sieci społecznych.

Model SIS

Model SIS na klasycznym grafie przypadkowym

Podstawowy modelem epidemiologicznym jest model SIS, który zakłada tylko dwa możliwe stany osobników:

$S$ (ang. $Susceptible$ ) - liczba zdrowych osobników, podatnych na zarażenie
$I$ (ang. $Infected$ ) - liczba zarażonych
W modelu tym nie uzwględnia się zatem nabywania odporności po przebyciu choroby.

W pierwszej kolejności omówimy zachowanie tego modelu na klasycznym grafie przypadkowym, czyli na sieci, która zakłada, że każdy węzeł ma taki sam stopień $\langle k \rangle$ (stopień węzła $k$ to liczba krawędzi łącząca dany węzeł z innymi węzłami). Innymi słowy, zakładamy, że każdy osobnik ma kontakt z jednakową liczbą innych osobników.

W modelu tym przyjmujemy również, że populacja osobników jest stała i wynosi $N$ , a co za tym idzie
$S(t) + I(t) = N$
Zmiany stanów osobników zachodzą według schematu: \\

$\beta$ - prawdopodobieństwo przekazania patogenu od chorego do zdrowego osobnika w przypadku ich kontaktu \\
$\gamma$ - prawdopodobieństwo, że chory osobnik wyzdrowieje

Równanie opisujące w jaki sposób zmienia się w czasie liczba zarażonych:

$\begin{equation*} \frac{dI(t)}{dt} = \beta \frac{\langle k \rangle I(t)}{N}S(t) - \gamma I(t) \end{equation*}$

Pierwszy człon prawej strony równania opisuje liczbę osobników, która w czasie $(t, t+dt)$ zmienia stan $S \longrightarrow I$ , czyli zachoruje, a sam wyraz ${\langle k \rangle I(t)}/{N}$ reprezentuje średnią liczbę chorych osobników, z którymi zdrowy osobnik ma kontakt. Drugi człon opisuje liczbę osobników, którzy w tym czasie wyzdrowieli, czyli zmienili stan $I \longrightarrow S$ . Pierwszy człon jest dodatni, bo zwiększa liczebność populacji I, a drugi jest na minusie, ponieważ ją zmniejsza.

Definiuje się \textbf{parametr tempa rozprzestrzeniania się epidemii} jako:

$\begin{equation*} \lambda = \frac{\beta}{\gamma} \end{equation*}$

Parametr ten odgrywa kluczową rolę w określeniu, czy rozprzestrzeniająca się infekcja stanie się epidemią, czy wygaśnie. Krytyczna wartość tego parametru określona jest jako:

$\begin{equation*} \lambda_C = \frac{N}{\langle k \rangle S_0} \end{equation*}$

przy czym $S_0$ z warunków początkowych $S(t = 0) = S_0$ jest początkową liczbą podatnych na zarażenie.
Dla przypadku, gdy liczba podatnych na zarażenie jest znacznie mniejsza od liczby wszystkich osobników w populacji $S_0 << N$ , krytyczne tempo rozprzestrzeniania epidemii wynosi

$\begin{equation*} \lambda_C = \frac{1}{\langle k \rangle} \end{equation*}$

czyli zależy tylko od struktury sieci.

dla $\lambda = \frac{\beta}{\gamma} < \lambda_C$ infekcja wygasa
dla $\lambda = \frac{\beta}{\gamma} > \lambda_C$ infekcja będzie się rozprzestrzeniała stając się epidemią

Sterując parametrami $\beta$ i $\gamma$ możemy sterować wartością tempa rozprzestrzeniania epidemii. Jeśli uda się zmniejszyć parametr $\lambda$ do wartości poniżej progu epidemii $\lambda_C$ , epidemia wygasa.

Aby zmniejszyć parametr $\beta$ , czyli prawdopodobieństwo zachorowania, w przypadku infekcji przenoszonej drogą kropelkową stosuje się działania typu:

częste mycie rąk
stosowanie maseczek, odzieży ochronnej
zasłanianie ust/nosa w przypadku kaszlu, czy kichnięcia
utrzymywanie odpowiedniej odległości od innych ludzi, nie tłoczenie się

Zwiększanie parametru $\gamma$ , czyli prawdopodobieństwa wyzdrowienia, zachodzi poprzez:

hospitalizację chorych
zwiększanie wydatków na sektor medyczny
wspieranie badań naukowych

Natomiast na zmniejszenie średniego stopnia węzła $\langle k \rangle$ , czyli zmniejszenie liczby kontaktów z innymi osobami, co zwiększa wartość krytycznego tempa rozprzestrzeniania się epidemii $\lambda_C$ wpływają:

izolacja chorych, stosowanie kwarantanny
ograniczenia w transporcie
zamknięcie placówek publicznych
praca zdalna

Można również nieco inaczej zdefiniować parametr, od którego zależy dynamika rozprzestrzeniania się infekcji, a mianowicie jako \textbf{bazowy współczynnik reprodukcji},a potocznie, głównie w mediach, nazywany \textbf{wskaźnikiem zaraźliwości} wirusa. Wyraża się on w stosowanej przez nas konwencji jako:

$\begin{equation*} R_0 = \frac{\beta \langle k \rangle S_0}{\gamma N} \end{equation*}$

{}Parametr ten mówi o tym, jaką średnią liczbę osób zaraża jedna osoba zarażona.
dla wartości $R_0 < 1$ epidemia wygasa
dla wartości $R_0 >1$ epidemia rozprzestrzenia się

Przykładowo bazowy współczynnik reprodukcji $R_0$ dla pandemii grypy hiszpanki (1918) wahał się w granicach $2-4.3$ , dla polio współczynnik ten wynosi $5-7$ , dla zwykłej grypy około $1.3$ , dla epidemii SARS (2002) $2-5$ , a dla wczesnych etapów pandemii wirusa SARS-CoV-2 (2019) wywołującego chorobę COVID-19, estymowano ten współczynnik na poziomie $2.35$ , ale z pewnością nie jest to wynik ostateczny i również w tym przypadku podaje się raczej zakres $2 - 3$ .

Model SIS na sieciach bezskalowych

Przejdźmy teraz do omówienia modelu SIS na sieciach bezskalowych. W sieciach bezskalowych nie ma założenia, że wszystkie węzły mają jednakową liczbę krawędzi, czyli ten sam stopień $k$ . Zamiast tego węzły mają różne stopnie, a ich rozkład przyjmuje postać potęgową:

$\begin{equation*} P(k) \sim k^{(-\gamma) } \end{equation*}$

przy czym wykładnik $\gamma \in [2,3]$ .
Oznacza to, że niektóre węzły mogą mieć bardzo dużą liczbę krawędzi, są to tzw. huby, a inne mogą mieć ich bardzo mało. Taka sieć jest dużo lepszym przybliżeniem rzeczywistych sieci społecznych niż omówiony wcześniej graf przypadkowy. W sieci kontaktów międzyludzkich liczba osób z jakimi ma się kontakt może się mocno różnić w zależności od osoby. Występują w niej huby, czyli osoby, które spotykają się z bardzo dużą liczbą osób, na przykład ze względu na wykonywany zawód, ale także osoby prawie całkowicie odizolowane, które spotykają bardzo mało osób.

W sieciach bezskalowych należy rozważać zatem liczbę podatnych i zarażonych osobników o zadanym stopniu $k$ :
$S_k(t)$ - liczba podatnych osobników o stopniu węzła $k$ w chwili $t$
$I_k(t)$ - liczba zarażonych osobników o stopniu węzła $k$ w chwili $t$

W tym przypadku znowu mamy stałą liczebność populacji, więc również stałą liczbę węzłów o stopniu $k$ :

$\begin{equation*} S_k(t) + I_k(t) = N_k = NP(k) \end{equation*}$

Należy jeszcze zdefiniować
$Q_I$ - prawdopodobieństwo, że dowolna krawędź ma połączenie z chorym węzłem

W tym przypadku równanie opisujące zmianę liczby zarażonych w czasie wyraża się:

$\begin{equation*} \frac{dI_k(t)}{dt} = \beta {(k Q_I) I_k(t)}S_k(t) - \gamma I_k(t) \end{equation*}$

W takich sieciach próg epidemii jest inny od progu w klasycznych grafach przypadkowych i wynosi:

$\begin{equation*} \lambda_C = \frac{\langle k \rangle}{\langle k^2 \rangle} \end{equation*}$

Co ważne dla sieci bezskalowych, które charakteryzują się potęgowym rozkładem węzłów ten próg wynosi

$\begin{equation*} \lambda_C \simeq 0 \end{equation*}$

Co ten wniosek oznacza w praktyce?
W sieciach bezskalowych całkowite wyeliminowanie choroby, czy też możliwości pojawienia się epidemii, jest praktycznie niemożliwe przy pomocy tradycyjnych metod typu masowe szczepienia, a sama epidemia jest bardzo trudna do opanowania. W takich sieciach wystarczy jeden zarażony węzeł o dużym stopniu, aby rozpocząć epidemię. Zatem w tym przypadku efektywną strategią wydaje się tropienie i eliminacja kluczowych węzłów - hubów.

Model SIR

Najszerzej stosowanym modelem epidemiologicznym jest model SIR, który uwzględnia nabywanie odporności po przebyciu choroby. Zakłada się możliwe stany osobników:
$S$ (ang. $Susceptible$ ) - liczba zdrowych osobników, podatnych na zarażenie
$I$ (ang. $Infected$ ) - liczba zarażonych
$R$ (ang. $Recovered$ ) - liczba osobników, którzy wyzdrowieli i są odporni na chorobę
Zmiany stanów osobników zachodzą według schematu: \\

$r$ - prawdopodobieństwo zarażenia osobnika zdrowego \\
$a$ - prawdopodobieństwo, że chory osobnik wyzdrowieje
W modelu tym znowu zakłada się stałą liczebność populacji:

$\begin{equation*} S(t) + I(t) + R(t) = N \end{equation*}$

Oznacza to, że osoby, które zmarły na skutek choroby uznaje się za uodpornione (R) i dalej się je zlicza.
Równania (Kermacka-McKendricka) opisujące rozprzestrzenianie się epidemii w czasie:

$\begin{equation*} \frac{dS}{dt} = - r S I \end{equation*}$

$\begin{equation*} \frac{dI}{dt} = r S I - a I \end{equation*}$

$\begin{equation*} \frac{dR}{dt} = a I \end{equation*}$

Zauważmy, że w pierwszy wzór opisuje zmianę liczby osobników podanych, która to zmniejsza się na skutek zachorowania, dlatego we wzorze występuje minus. Drugi wzór opisuje zmianę liczby zainfekowanych osobników, która zwiększa się na skutek zachorowanie (człon $r S I$ ) i zmniejsza na skutek wyzdrowienia (człon $-a I$ ). Ostatni wzór opisuje zmianę liczby wyzdrowiałych, która to zwiększa się, gdy chory z prawdopodobieństwem $a$ wyzdrowieje.

Model ten można dowolnie modyfikować tak, aby jak najlepiej charakteryzował konkretny patogen. Przykładową modyfikacją jest model SEIR, który uwzględnia dodatkowo stan \textbf{E} (and. \textit{Exposed}) reprezentujący osobników w przejściowym, utajonym stadium choroby, czyli zarażających innych osobników, ale nie mających żadnych objawów choroby. Tutaj zmiany stanów następują według schematu:

Krzywa epidemiologiczna

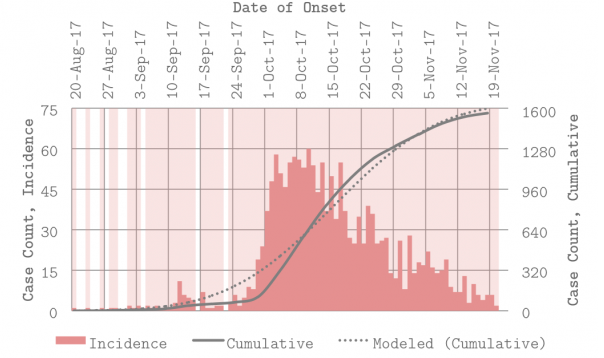
Rysunek jest częścią pracy: Majumder M.S., Cohn E.L., Santillana M., Brownstein J.S., Estimation of Pneumonic Plague Transmission in Madagascar}, August–November 2017. PLOS Currents Outbreaks. 2018 Nov 1. Edition 1

Przykładowa krzywa epidemiologiczna. Przedstawia dane dotyczące epidemii dżumy płucnej na Madagaskarze. Na różowo został przedstawiony histogram liczby nowych przypadków zachorowań w ciągu danego dnia. Szarą linią ciągłą przedstawiono sumę dotychczasowych zarażeń. Szara linia przerywana jest sumą wszystkich zachorowań wyznaczoną z modelu dla wartości bazowego współczynnika reprodukcji $R_0 = 2.4$

Przedstawiając dane dotyczące dynamiki epidemii w postaci liczby zachorowań stosuje się krzywą epidemiologiczną, którą może przyjąć dwie postacie widoczne na Rysunku 1. Pierwszą z nich jest przedstawiony na rysunku kolorem różowym histogram, który pokazuje ile nowych przypadków zachorowań zaobserwowano w ciągu jednego dnia. Krzywa ta z reguły jest dość nieregularna, ale ma dzwonowaty kształt z jednym lub wieloma maksimami. Drugą postacią krzywej epidemiologicznej jest skumulowana suma zachorowań, zaznaczona na Rysunku 1. jako szara linia ciągła. Pokazuje ona ile dotychczas wystąpiło wszystkich zachorowań. Jest zawsze krzywą rosnącą, która na końcu, gdy liczba przypadków występujących w ciągu jednego dnia się zmniejsza, wygładza się.

Pandemia

Pandemią nazywamy taki rodzaj epidemii, który objął ogromny obszar, wiele kontynentów lub też cały świat i dotknął znaczną część ziemskiej populacji. Wcześniej WHO wyszczególniało konkretne fazy w rozprzestrzenianiu się infekcji, które prowadziły do pandemii, ale odeszło się od tego.

Czynnikami, które sprzyjają wystąpieniu pandemii są:

niska śmiertelność
duża wartość bazowego współczynnika reprodukcji $R_0 \gg 0$
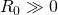
długi okres inkubacji choroby, czyli etapu bezobjawowego
brak naturalnej odporności populacji, czyli sytuacja, gdy patogen występuje po raz pierwszy lub nie występował od bardzo dawna
niegroźne objawy choroby

Przykładami występujących dotychczas pandemii były:

pandemia dżumy, znana również jako Czarna Śmierć (XIV wiek)
pandemia cholery (XIX wiek)
pandemia grypy hiszpanki (1918)
HIV/AIDS (występująca po dzień dzisiejszy)
pandemia wirusa A/H1N1v, znanego jako wirus świńskiej grypy (2009)
pandemia wirusa SARS-CoV-2 (2019)

Tagged under: covid-19, epidemia, krzywa, modelowanie, sieci