Kinematyka
Położenie – określa umiejscowienie ciała w przestrzeni względem wybranego układu odniesienia
Przemieszczenie – różnica pomiędzy początkowym położeniem ciała a końcowym
Tor ruchu – linia, po której porusza się ciało
Droga – długość toru ruchu
Ruch – zmiana położenia ciała w czasie
Rodzaje ruchu:
-
ze względu na kształt toru :
prostoliniowy
krzywoliniowy (np. po okręgu, elipsie)
-
ze względu na zależność przebytej drogi od czasu:
jednostajny – prędkość się nie zmienia
zmienny – prędkość się zmienia
jednostajnie zmienny – zmiany prędkości są jednakowe w jednakowych przedziałach czasu (jednostajnie przyspieszony lub jednostajnie opóźniony)
niejednostajnie zmienny
Ruch jednostajny prostoliniowy
- prędkość ciała nie zmienia się
- tor ruchu jest linią prostą
Prędkość w ruchu jednostajnym prostoliniowym :
v = s/t
s – droga przebyta przez ciało
t – czas, w jakim ciało przebyło tę drogę
Jednostką prędkości jest:
[v] = 1 m/s
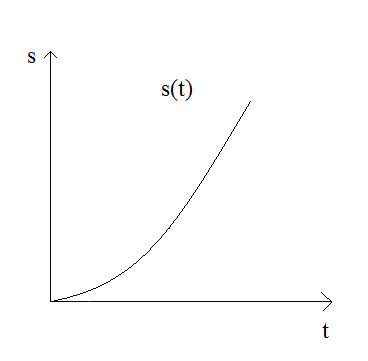
Wykres drogi od czasu s(t)
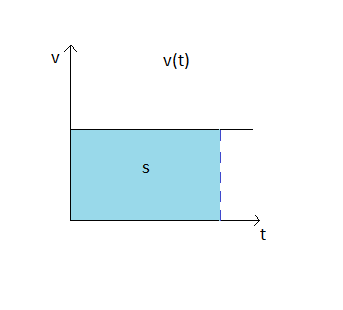
Wykres prędkości od czasu v(t)
Ruch jednostajnie zmienny prostoliniowy
Przyspieszenie – wyraża zmianę wektora prędkości w czasie
a = Δv/Δt
Δv – zmiana prędkości
Δt – czas w jakim nastąpiła ta zmiana
Jednostką przyspieszenia jest:
[a] = 1 m/s²
Cechy ruchu jednostajnie zmiennego prostoliniowego:
- przyspieszenie jest stałe
- ciało porusza się po linii prostej
Dla ruchu przyspieszonego a>0
Dla ruchu opóźnionego a<0 i jego wartość zapisujemy z minusem
Prędkość w chwili tk: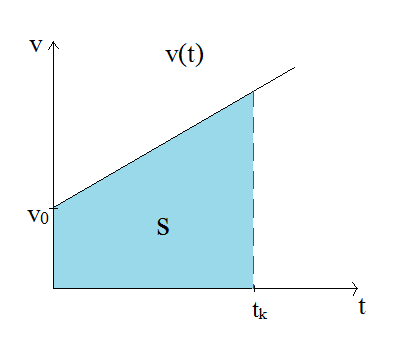
v(tk) = v0 + at
v0 - prędkość początkowa
a – przyspieszenie
t – czas, który minął do chwili tk
Droga, czyli wartość przesunięcia ciała do chwili tk:
s(tk) = v0t + at²/2
v0 - prędkość początkowa
a – przyspieszenie
t – czas, który minął do chwili tk
Ruch zmienny po okręgu
Ruch po okręgu jest z definicji ruchem zmiennym, nawet, jeżeli wartość prędkości się nie zmienia, ze względu na zmiany kierunku i zwrotu wektora prędkości.
α = ł/r
[α] = 1 rad (radian)
2Π = 360˚
Π = 180˚
Π/2 = 90˚
W ruchu po okręgu występuje prędkość kątowa, którą definiujemy: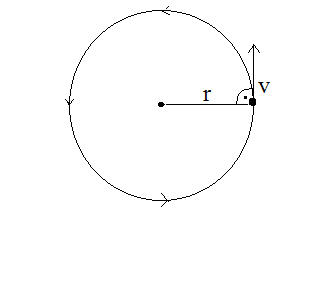
ω = α/t
[ω] = 1 rad/s
v = ω ∙ r
wektorowo:
v = ω × r
v – prędkość liniowa
r – promień okręgu
ω - prędkość kątowa
Przyspieszenie kątowe
ε = Δω/t
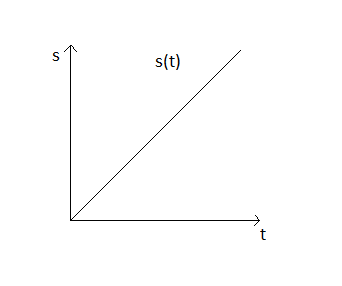


 (455 votes, average: 4,28 out of 5)
(455 votes, average: 4,28 out of 5)