Dynamika bryły sztywnej
Dynamika bryły sztywnej to jeden z elementarnych działów fizyki, dowiedz się więcej na temat jej kluczowych zagadnień.
Dynamika bryły sztywnej wzory i analiza
Bryła sztywna – ciało, którego punkty nie przemieszczają się względem siebie.
W ruchu obrotowym bryły sztywnej każdy punkt bryły zatacza okrąg o środku leżącym na osi obrotu bryły.
Odległość punktu od osi obrotu (oznaczane jako r) - to najkrótszy odcinek łączący punkt i oś obrotu.
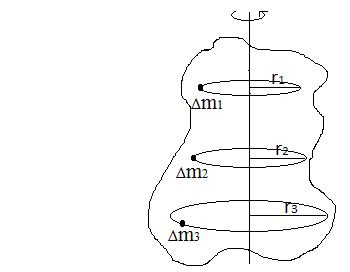 Δm – masa elementarna = punkt materialny
Δm – masa elementarna = punkt materialny
r – odległość punktu od osi obrotu
v1 = ω·r1 … vn = ω·rn
Każdy punkt bryły ma tę samą prędkość kątowa ω i różną prędkość liniową v.
Moment bezwładności – suma iloczynów mas elementarnych i kwadratu ich odległości od osi obrotu, zależna od osi obrotu.
I = Δm1·r1² + Δm2·r2² + ... + Δmn·rn²
[I] = 1 kg·m²
Im dalej jest rozłożona masa bryły od osi obrotu, tym większy jest moment bezwładności.
Momenty bezwładności przykładowych brył:
- kula: I = 2/5·mR²,R – promień kuli
- sfera: I = 2/3·mR²
- walec: I = 1/2·mR²
- rury cienkościennej: I = mR²
- pręt, którego oś obrotu przechodzi przez środek jego długości: I = 1/12·mL² (L – długość pręta)
- pręt, którego oś obrotu przechodzi przez jeden z jego końców: I = 1/3·mL²
Porównanie ruchu postępowego i ruchu obrotowego
Zasady dynamiki dla ruchu obrotowego bryły sztywnej
I zasada dynamiki:
Jeżeli wypadkowy moment siły M działający na ciało jest równy zero, to prędkość kątowa ω ciała jest stała lub równa zero.
Uogólnienie I zasady dynamiki:
Jeżeli wypadkowy moment siły M działający na ciało jest równy zero, to moment pędu L ciała jest stały.
II zasada dynamiki Newtona:
Jeżeli wypadkowy moment siły M działający na ciało nie jest równy zero, to ciało porusza się z przyspieszeniem kątowym równym ε = M/I.
Uogólnienie II zasady dynamiki:
Zmiana momentu pędu ciała jest równa
Δk=M·t
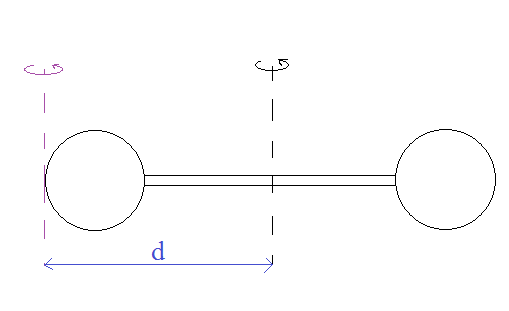
Twierdzenie Steinera
I = I0 + md²
I0 – moment bezwładności względem osi przechodzącej przez środek masy
I – moment bezwładności względem osi równoległej do pierwszej osi
d – odległość między osiami
m – masa bryły
Zasada zachowania momentu pędu
Moment pędu bryły w układzie inercjalnym pozostaje stały, gdy nie działa na nią żaden moment siły zewnętrznej.
Iω = const
I1ω1 = I2ω2
Zasadę wykorzystują np. łyżwiarze robiąc piruet. Gdy łyżwiarka ma rozłożone ręce obraca się powoli, kiedy z kolei składa ręce blisko siebie, obraca się znacząco szybciej. Dzieje się tak dlatego, że moment bezwładności łyżwiarki przy składaniu rąk maleje, musi więc rosnąć prędkość kątowa.

 (651 votes, average: 4,27 out of 5)
(651 votes, average: 4,27 out of 5)