Zadania z elektryczności
1.1
Oblicz natężenie prądu wytworzonego przez elektron krążący z częstotliwością 45![]() na pierwszej orbicie w atomie wodoru. Ładunek elektronu jest równy
na pierwszej orbicie w atomie wodoru. Ładunek elektronu jest równy ![]() .
.
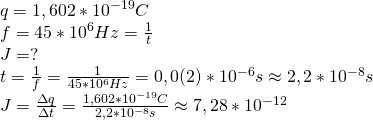
1.2
Poniższe wykresy przedstawiają zależność o czasu natężenia prądu przepływającego przez przekrój poprzeczny przewodnika. W każdym przypadku oblicz przybliżoną liczbę elektronów, które przepłynęły przez przekrój poprzeczny przewodnika w czasie 20 sekund.
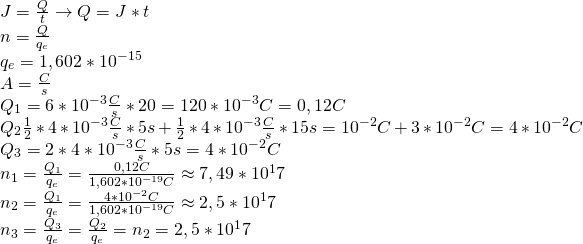
1.3
Wykres przedstawia zależność ładunku elektrycznego przepływającego przez pewien przewodnik od czasul Na jego podstawie oblicz natężenie prądu płynącego w tym przewodniku,
![]()
1.4
Działko elektronowe jest źródłem strumienia elektronów. Oblicz masę elektronów wypływających z działka w czasie ![]() , jeżeli natężenie prądu elektronów z działka wynosi
, jeżeli natężenie prądu elektronów z działka wynosi ![]() .
.
Do obliczeń przyjmij, że stosunek ![]() .
.
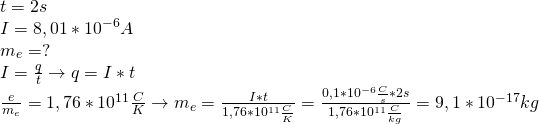
1.5
Przewodnik o oporze ![]() włączono do źródła napięcia
włączono do źródła napięcia ![]() . Oblicz czas w którym przez przewodnik przepłynął ładunek
. Oblicz czas w którym przez przewodnik przepłynął ładunek ![]() .
.
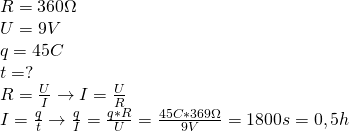
Działania na jednostkach:
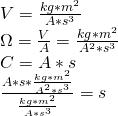
1.6
Przez przewodnik o oporze ![]() płynie prąd o natęrzeniu
płynie prąd o natęrzeniu ![]() . Oblicz wartość natężenia pola elektrycznego w tym przewodniku. jeżeli jego długość wynosi
. Oblicz wartość natężenia pola elektrycznego w tym przewodniku. jeżeli jego długość wynosi ![]() . Pole przekroju poprzecznego przewodnika jest na całej długości jednakowe.
. Pole przekroju poprzecznego przewodnika jest na całej długości jednakowe.
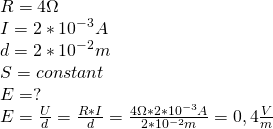
Działnie na jednostkach:
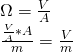
1.7
Opór kawałka drutu wynosi ![]() . Oblicz opór drugiego kawałka drutu wykonanego z tego samego materiału, ale o średnicy trzy razy mniejszej i dwa razy większej długości.
. Oblicz opór drugiego kawałka drutu wykonanego z tego samego materiału, ale o średnicy trzy razy mniejszej i dwa razy większej długości.
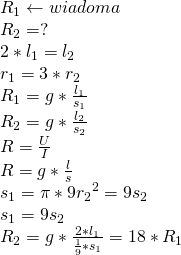
1.8
Opór elektryczny włókna wolframowego żarówki rozgrzanego do temperatury ![]() wynosi
wynosi ![]() , a jego długość
, a jego długość ![]() . Oblicz średnicę włókna, jeżeli opór właściwy wolframu w tej temperaturze jest równy
. Oblicz średnicę włókna, jeżeli opór właściwy wolframu w tej temperaturze jest równy ![]() .
.
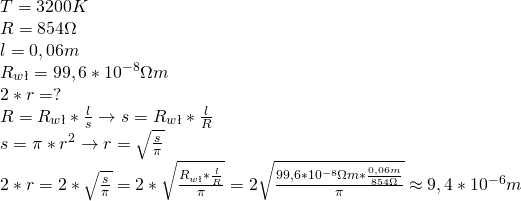
1.9
Do wykonania przewodów elektrycznych wykorzystano drut z miedzi o całkowitym oporzer ![]() i masie
i masie ![]() . Oblicz, jak długi będzie przewód elektryczny z tego drutu. Przyjmij, że opór właściwy miedzi wynosi
. Oblicz, jak długi będzie przewód elektryczny z tego drutu. Przyjmij, że opór właściwy miedzi wynosi ![]() , a jej gęstoś jest równa
, a jej gęstoś jest równa ![]() .
.
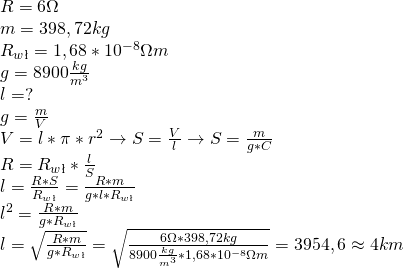
1.10
Do końców miedzianego przewodnika o masie ![]() i średnicy
i średnicy ![]() przyłożono napięcie
przyłożono napięcie ![]() . Oblicz natężenie prądu, który popłynie w przewodniku, jeżeli opór właściwy miedzi wynosi
. Oblicz natężenie prądu, który popłynie w przewodniku, jeżeli opór właściwy miedzi wynosi ![]() , a jej gęstoś jest równa
, a jej gęstoś jest równa ![]() . Przyjmij, że
. Przyjmij, że ![]() .
.
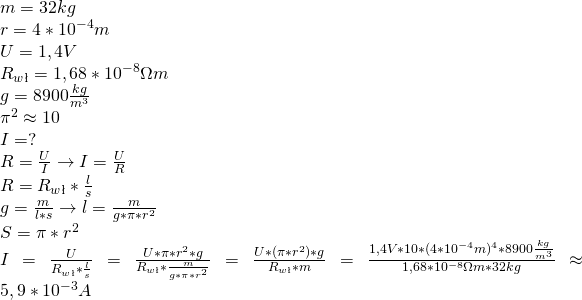
Działania na jednostkach:
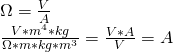
1.11
Pręt aluminium o gęstości ![]() i oporze właściwym
i oporze właściwym ![]() ma osiem razy mniejszy opór od oporu pręta z grafitu o gęstości
ma osiem razy mniejszy opór od oporu pręta z grafitu o gęstości ![]() i oporze właściwym
i oporze właściwym ![]() . Oblicz, ile razy dłuższy jest pręt z aluminium, jeżeli ich masy są jednakowe.
. Oblicz, ile razy dłuższy jest pręt z aluminium, jeżeli ich masy są jednakowe.
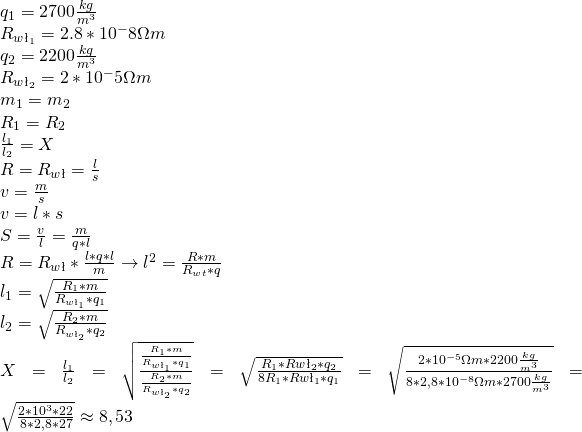
1.12
Wykres przedstawia zależność natężenia prądu płynącego przez przewodnik o długości ![]() od natężenia pola elektrycznego w tym przewodniku.
od natężenia pola elektrycznego w tym przewodniku.
Na jego podstawie oblicz opór przeodnika, wiedząć, że przewodnik ma wszędzie jednakową średnicę.
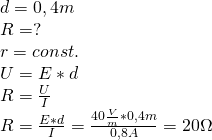
1.14
Przez przewodnik z miedzi o oporze właściwym ![]() i promieniu przekroju
i promieniu przekroju ![]() płynie prąd o natężeniu
płynie prąd o natężeniu ![]() . Oblicz długość tego przewodnika, jeżeli w czasie jednej sekundy oddaje on do otoczenia
. Oblicz długość tego przewodnika, jeżeli w czasie jednej sekundy oddaje on do otoczenia ![]() energii.
energii.
![Rendered by QuickLaTeX.com \\ l = ? \\ R_{wł} = 1,68 * 10^{-8} \ohm m \\ U = I * R \\ R = R_{wł} * \frac{l}{s} \\ R = \frac{U}{I} \\ W = E * q * l \\ U = E * l \rightarrow W = U * q \\ I = \frac{q}{t} \rightarrow q = I*t \\ r = 0,75 * 10^[-]m \\ I = 20A \\ S = \pi r^2 \\ t = 1s \\ W = \Delta E_{pot} = 1075,2 J \\ W = I * R_{wł} * \frac{l}{\pi r^2} * q \\ W = I^2 * R_{wł} * \frac{l}{\pi r^2} * t \\ l = \frac{W * \pi r^2}{I^2 * R_{wł} * t} = \frac{1075,2J * \pi *(7,5 * 10^{-4}m)}{(20A)^2 * 1,68 * 10^{-8}\ohm m * 1s} \approx 282,74m \\\\](https://fizyka.uniedu.pl/wp-content/ql-cache/quicklatex.com-cce9521dab1412168ffe29b96e1b4ef0_l3.png)
Działania na jednostkach:
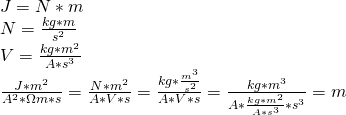
1.15
Oblicz, ile ciepła przekaże wodzie czajnik elektryczny o mocy 2![]() dołączony do źródła o napięciu
dołączony do źródła o napięciu ![]() w czasie 1,5 min. Straty grzałki czajnika szacuje się na
w czasie 1,5 min. Straty grzałki czajnika szacuje się na ![]() .
.
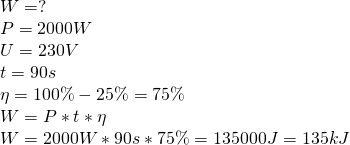
1.16
Przez uzwojenie silnika lokomotywy płynie prąd o natężeniu ![]() . Lokomotywa wraz z całym składem porusza się z szybkością
. Lokomotywa wraz z całym składem porusza się z szybkością ![]() , a jej siła ciągu wynosi
, a jej siła ciągu wynosi ![]() . Oblicz napięcie, które zasila silnik lokomotywy, jeśli
. Oblicz napięcie, które zasila silnik lokomotywy, jeśli ![]() energii elektrycznej zamienione zostaje na pracę silnika.
energii elektrycznej zamienione zostaje na pracę silnika.
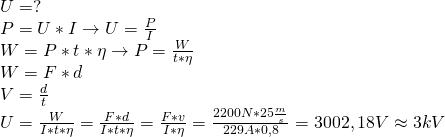
Działania na jednostkach:
![]()
1.17
Za pomocą dzwigu podnoszono ruchem jednostajnym betonową płytę o gęstości ![]() i wymiarach
i wymiarach ![]() x
x ![]() x
x ![]() . Straty energii podczas podnoszenia płyty wynoszą około
. Straty energii podczas podnoszenia płyty wynoszą około ![]() . Oblicz wartość prędkości, z którą podnoszono płytę, jeżeli przy napięciu zasilającym
. Oblicz wartość prędkości, z którą podnoszono płytę, jeżeli przy napięciu zasilającym ![]() przez silnik płynął prąd o natężeniu
przez silnik płynął prąd o natężeniu ![]() .
.
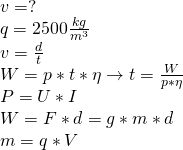
Wymiary: ![]() x
x ![]() x
x ![]()
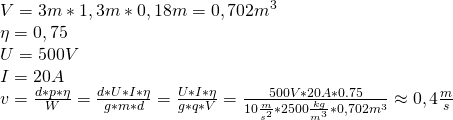
Działania na jednostkach:
![]()
1.18
Za pomocą grzałki elektrycznej w czasie ![]() zagotowano pół litra wody, której temperatura początkowa wynosiła
zagotowano pół litra wody, której temperatura początkowa wynosiła ![]() . Oblicz moc grzałki, jeżeli jej sprawność wynosi
. Oblicz moc grzałki, jeżeli jej sprawność wynosi ![]() . Ciepło właściwe wody jest równe 4200\frac{J}{kgK}.
. Ciepło właściwe wody jest równe 4200\frac{J}{kgK}.

Działania na jednostkach:
![]()
1.19
Kontener o masie 1,2 tony wciągano ruchem jednostajnym z szybkością ![]() po równi pochyłej za pomocą silnika elektrycznego.
po równi pochyłej za pomocą silnika elektrycznego.
Silnik elektryczny połączono z kontenerem nierozciągliwą liną, którą przerzucono przez nieruchomy blok. Oblicz sprawność silnika, jeżeli jego moc jest równa ![]() Przyjmij, że współczynnik tarcia kontenera o równię wynosi 0,2.
Przyjmij, że współczynnik tarcia kontenera o równię wynosi 0,2.
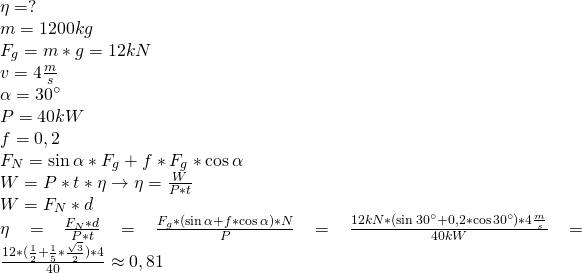
Działania na jednostkach:
![]()
1.20
Oblicz opory zastępcze poniższych układów odbiorników.
a)
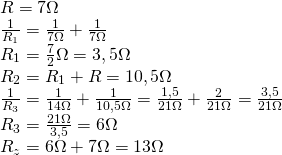
b)
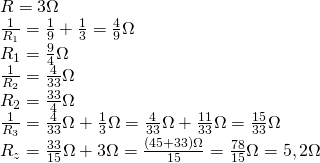
c)
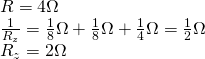
d)
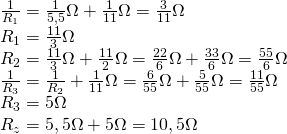
e)
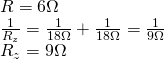
f)

 (252 votes, average: 4,28 out of 5)
(252 votes, average: 4,28 out of 5)