Wektory i skalary

 

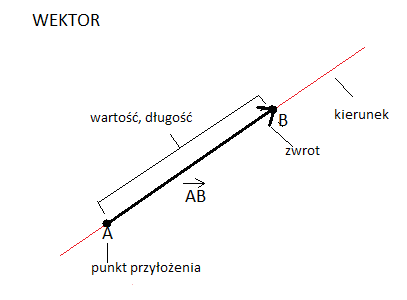
WIELKOŚCI FIZYCZNE
	Skalar	Wektor
Charakteryzuje go	wartość	wartość – długość wektora kierunek zwrot punkt przyłożenia
Przykłady	temperatura, długość, objętość, masa, energia	prędkość, siła, pęd

Wektor wyraża się jako:

a = [x2 - x1 , y2 – y1]

Wielkość wektorową będziemy oznaczać pogrubioną kursywą, np. v, a, F
A jej wartość (długość wektora) niepogrubioną, czyli np. v, a, F.

---

Działania na wektorach: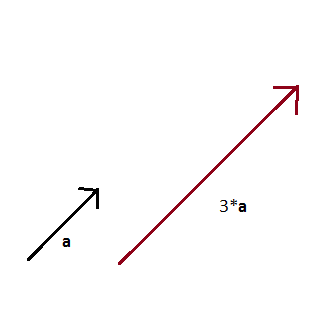

Mnożenie wektora przez skalar

np. 3·a

a = [ x, y]

3·a= [ 3x, 3y]

---

Dodawanie wektorów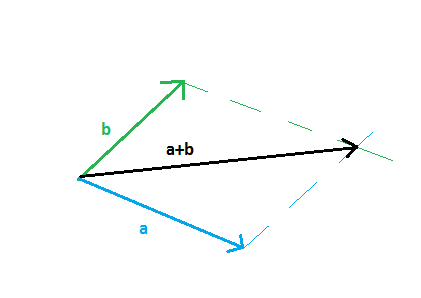

a+b=c

a = [ x(a) , y(a)]

b = [ x(b) , y(b)]

a+b = [x(a) + x(b), y(a)+y(b)]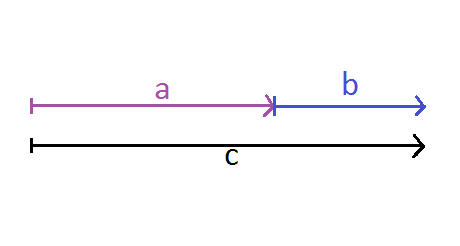

---

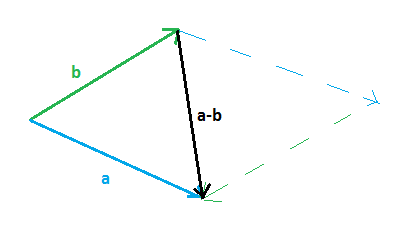Odejmowanie wektorów (dodajemy wektor przeciwny -b)

a – b = d

a – b = [ x(a) – x(b), y(a) – y(b)]

 

---

Iloczyn skalarny

a·b = |a|·|b|·cosΘ

a = [x(a) , y(a)]

b = [x(b) , y(b)]

a·b = x(a)·x(b) + y(a)·y(b)

Θ – kąt pomiędzy wektorami a i b
|a| - długość wektora a
|a| = √x(a)² + y(a)²

Iloczyn skalarny jest przemienny

a·b = b·a

Wynikiem iloczynu skalarnego jest skalar, czyli liczba.

---

Iloczyn wektorowy

Warość bezwzględna iloczynu wektorowego

|a×b| = |a|·|b|·sinΘ 

Θ – kąt pomiędzy wektorami a i b

Iloczyn wektorowy nie jest przemienny

a×b = -b×a

Wynikiem iloczynu wektorowego jest wektor prostopadły do wektora a i wektora b.

---

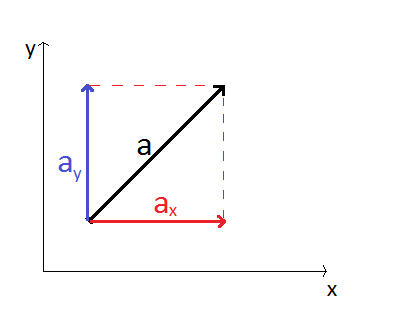
Rozkładanie wektora na składowe

a = a_x + a_y