6. Fale mechaniczne - fale dzwiękowe
Fala dźwiękowa – dowolna fala podłużna rozchodząca się w ośrodku sprężystym
Ton – sinusoidalna fala dźwiękowa o ściśle określonej częstotliwości, amplitudzie i fazie
Rozchodzenie się fali dźwiękowej:
- gazy i ciecze: przemieszczanie się zagęszczeń i rozrzedzeń ośrodka
- ciała stałe: rozchodzenie się odkształceń lub naprężeń mechanicznych
Natężenie dźwięku
I = P/S
P – moc dźwięku
S – pole powierzchni, na którą pada fala
[I] = 1 W/m²
Częstotliwości fal dźwiękowych, które są słyszalne dla ludzkiego ucha:
16 Hz – 20000 Hz
Poniżej 16 Hz – infradźwięki
20000 Hz – 1 GHz – ultradźwięki
Powyżej 1 GHz – hiperdźwięki
Poziom natężenia dźwięku
β = 10·log(I/I0)
I – natężenie dźwięku
Io – dolny próg słyszalności – minimalne natężenie dźwięku o f = 1 kHz, przy którym w uchu ludzkim pojawia się wrażenie dźwiękowe
I0 = 10-12 W/m²
[β] = 1 dB (decybel) = 10 B (bel)
Prędkość dźwięku w powietrzu wynosi około 340 m/s.
Rezonans akustyczny - zjawisko wzrostu amplitudy drgań źródła dźwięku (np. struny) zachodzące przy ściśle określonych wartościach częstości (tzw. rezonansowych)
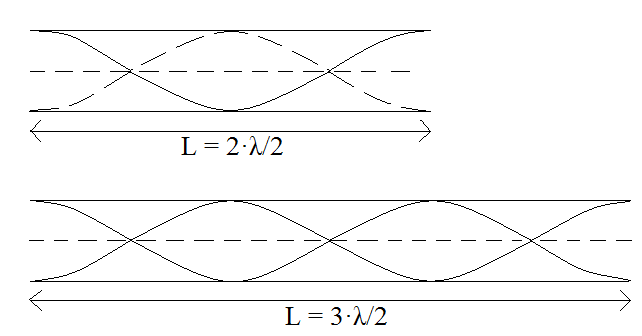
Drgania rezonansowe struny
warunek fali stojącej:
L = n·λ/2
n = 1, 2, 3, …
Drganie rezonansowe w piszczałce
- piszczałka obustronnie otwarta
L = n·λ/2
n = 1, 2, 3, …
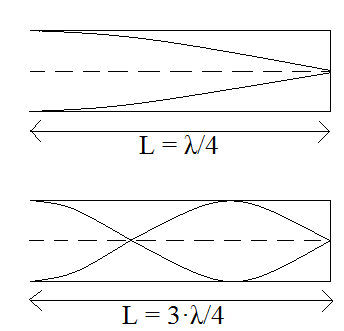
- piszczałka jednostronnie zamknięta
L = n·λ/4
n = 1, 3, 5, …
Zjawisko Dopplera dla fal dźwiękowych - zmiana odbieranej częstotliwości dźwięku spowodowana ruchem źródła dźwięku i/lub obserwatora
f ' - częstotliwość odbierana przez obserwatora
f – częstotliwość źródła fali
v – prędkość dźwięku
w – prędkość obserwatora
u – prędkość źródła
Jeśli obserwator zbliża się do źródła w liczniku stawiamy znak '+', a jeśli się oddala znak '-'.
Jeśli źródło zbliża się do obserwatora w mianowniku stawiamy znak '-', a jeśli się oddala znak '+'.
Ciała poruszające się szybciej od dźwięku
np. samoloty, pociski naddźwiękowe
Liczba Macha
M = u/vdź
u – prędkość źródła dźwięku
vdź – prędkość rozchodzenia się dźwięku w danym ośrodku
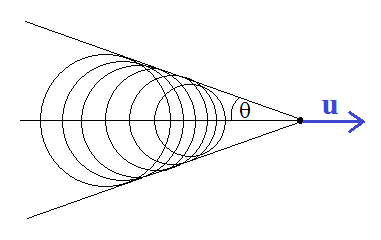
Powstawanie fali uderzeniowej tworzącej tzw. stożek Macha
sinΘ = 1/M
M – liczba Macha

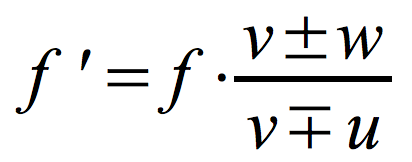

 (451 votes, average: 4,32 out of 5)
(451 votes, average: 4,32 out of 5)