4. Wahadło matematyczne, drgania tłumione i wymuszone
Wahadło matematyczne – punktowa masa zawieszona na nieważkiej i nierozciągliwej nici
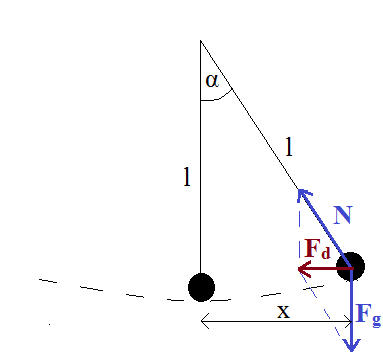 dla małych kątów wychylenia → przybliżenie ruchu w poziomie:
dla małych kątów wychylenia → przybliżenie ruchu w poziomie:
tgα ≈ x/l
Fd = Fg·tgα = m·g·x/l
ruch harmoniczny:
Fd = Fs
- m·g·x/l = - k·x → k = mg/l
Izochronizm drgań wahadła – okres drgań nie zależy od ich amplitudy
Drgania tłumione – amplituda maleje w czasie na skutek działania zewnętrznych sił tłumiących.
Najczęstsza reprezentacja siły tłumienia:
F = -b·v
v – prędkość
b – współczynnik wprostproporcjonalności
Drgania wymuszone - drgania (tłumione), których amplituda jest podtrzymywana przez okresowo zmienną siłę wymuszającą.
Siła wymuszająca:
F = P·cos(ωt)
P – stała amplituda
ω – częstość siły wymuszającej
Rezonans mechaniczny – wzrost amplitudy drgań występujący przy określonej, tak zwanej rezonansowej częstości drgań ω, rezonans następuje gdy dwa układy drgające mają zbliżone częstości drgań własnych.
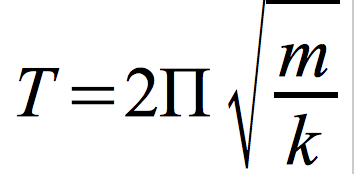

 (551 votes, average: 4,31 out of 5)
(551 votes, average: 4,31 out of 5)