Wektory jako sposób opisu rzeczywistości w fizyce

Wektory stanowią wielkości fizyczne, mające wartość, kierunek, zwrot i punkt przyłożenia. Sprawdzając temperaturę otoczenia, określamy tylko jej wartość bezwzględną i znak (czy jest na plusie, czy na minusie). Analizując ruch jadącego na wprost samochodu, nie musimy się zastanawiać nad wieloma jego aspektami. W istocie może się poruszać tylko w dwóch kierunkach – do przodu i do tyłu. Jednakże, zastanawiając się nad ruchem pszczoły, jak zdefiniujemy jego kierunek? Jego dwuwymiarowy opis nam już nie wystarczy. Z pomocą przyjdą nam jednak wektory.

Wektory i wielkości wektorowe

Kiedy rozpatrujemy wielkości, które mają postać pola, np. pole magnetyczne czy grawitacyjne, używamy do tego celu pola wektorowego. Z definicji jest to funkcja, która dla każdego punktu w przestrzeni przydziela jakąś wielkość wektorową. Innymi słowy, jeśli w każdym miejscu mamy określony wektor, czy natężenia danej wielkości, czy to siły przez nią wywieranej, to taki obszar będzie polem wektorowym. Takie pole możemy nazwać jednorodnym, gdy wektory w nim będą jednakowe, to znaczy będą miały ten sam kierunek, wartość i zwrot. Opisujemy jego gradient, czyli wzrost bądź spadek tej wielkości w określonym kierunku, dywergencję, czyli rozbieżność pola wektorowego oraz rotację, czyli regularną zmianę jego kierunku. Jakie to ma znaczenie? Przykładowo, przepływ prądu jest skutkiem gradientu pola elektrycznego.

Skoro wielkości wektorowe są odmienne w swojej definicji, można się spodziewać, że i inny będzie sposób przeprowadzania na nich działań. Omówmy je teraz. Zacznijmy od najprostszej operacji, czyli dodawania wektorów. Załóżmy, że przykładowa cząstka poruszyła się z punktu A do B, a potem skręciła pod kątem prostym, przemieszczając się do punktu C. Jak teraz policzyć jej całkowite przemieszczenie? Nie możemy przecież dodać tego skalarnie.

Kiedy jednak dysponujemy kartką papieru, możemy je zsumować w bardzo prosty sposób. Należy narysować wektory pod odpowiednim kątem względem siebie i w wygodnej skali i narysować wektor łączący końce tych dwóch, które dodajemy. Powstały odcinek należy następnie zmierzyć i przemnożyć przez wybraną przez nas skalę. Przy tych operacjach warto pamiętać, że tak jak przy wartościach skalarnych, wektorowe dodawanie jest przemienne. Możemy je także wykonywać w dowolnej kolejności. Także, jeżeli to będzie wygodniejsze przy naszych obliczeniach, wektor można przenieść na drugą stronę równania, byle z przeciwnym znakiem. A jak to by się miało do naszego rysunku? Taki odwrócony wektor będzie miał taki sam kierunek, lecz przeciwny zwrot.

Dodawanie wektorów algebraicznie

Co jednak gdy nie dysponujemy miejscem na rysunek? Lub mamy po prostu tyle wektorów, że zajęłoby nam to zbyt dużo czasu? Z pomocą przyjdzie nam algebraiczne dodawanie wektorów. W tym celu należy go rozbić na składowe, czyli na części wyznaczone względem każdej z osi. Jeśli rozbijemy wektor a według osi x (zwyczajowo przyjmowanej jako poziomą) i osi y (pionowej) otrzymamy składowe, których długości będą wynosiły odpowiednio a*cosφ i a*sinφ, gdzie φ to kąt, jaki wektor a tworzy z dodatnim kierunkiem osi x, a „a” oznacza jego długość.

Stosunek składowej pionowej do poziomej określa nam tangens kąta φ. Nasuwa nam to jeszcze jedno pytanie, mianowicie, skąd wiemy, że z tego stosunku określiliśmy poprawny kąt? Przykładowo, tangens równy 1,5 mamy dla kąta o mierze 86 stopni, jak i 236 stopni. Wszakże funkcja tangens jest okresowa. Cóż, to zależy tylko i wyłączenie od warunków zadania. Wynik otrzymany na kalkulatorze, czy wzięty z tablic należy skonfrontować z poleceniem. A co, gdybyśmy rozpatrywali wektor w trójwymiarze? Wtedy rozbilibyśmy go na 3 składowe i 2 kąty.

Wektor jednostkowy

Zanim przejdziemy do przedstawienia przepisu na dodawanie algebraiczne, wprowadźmy jeszcze pojęcie wektora jednostkowego, inaczej wersora. Jest to wektor, który nie ma jednostki ani wymiaru, jedynie jest skierowany w określonym kierunku i ma długość równą 1. Jaki jest zatem cel jego istnienia? Służy on do wskazywania kierunku. Dla osi x, y, z istnieją wektory jednostkowe nazwane odpowiednio i, j, k. Ułatwiają one i ujednolicają zapis innych wektorów. Wreszcie, jak dodajemy je do siebie? Bardzo prosto – po prostu sumujemy ich składowe.

Wynik możemy zapisać na dwa sposoby. Albo zaprezentujemy go za pomocą wcześniej wspomnianych wektorów składowych lub wyrazimy go poprzez jego moduł i kąt. Czym jest moduł? Jest to pierwiastek z sumy kwadratów składowych. Z kolei kąt możemy poznać dzięki odwrotności tangensa, funkcji arcus tangens. Podstawiając do niej wartość tangensa kąta (który wyliczymy ze składowych, jak wcześniej zostało wspomniane) otrzymamy jego wartość. Jeżeli otrzymamy wynik ujemny, oznacza, że jego wartość została zmierzona w kierunku przeciwnym do ruchu wskazówek zegara.

Jak mnożymy wektory?

Zajmijmy się teraz mnożeniem wektorów. Najprostszy przypadek to taki, w którym wymnażamy wektor przez jakiś skalar. Jego moduł będzie równy iloczynowi jego poprzedniej długości oraz wartości bezwzględnej skalara s. Dlaczego akurat wartość bezwzględna? Dzieje się tak dlatego, że znak liczby s będzie miał wpływ na zwrot wektora. Gdy s będzie dodatnie, pomnożony wektor będzie miał taki sam zwrot jak wcześniejszy, przy ujemnym zwrot będzie przeciwny. W przypadku mnożenia przez siebie dwóch wektorów sprawa nie jest już taka prosta. Możemy wyliczyć bowiem zarówno ich iloczyn skalarny, jak i wektorowy.

W przypadku tego pierwszego sprawa jest mniej skomplikowana – mnożymy bowiem moduły dwóch wektorów i cosinus kąta między nimi. Z tego też mamy uzasadnienie nazwy tego iloczynu, wszystkie bowiem te wartości są skalarami. Jest on przemienny i gdy rozpiszemy go na wektory jednostkowe, zauważymy, że w nowym wektorze wszystkie składowe będą iloczynami składowych czynników.

Na czym polega iloczyn wektorowy?

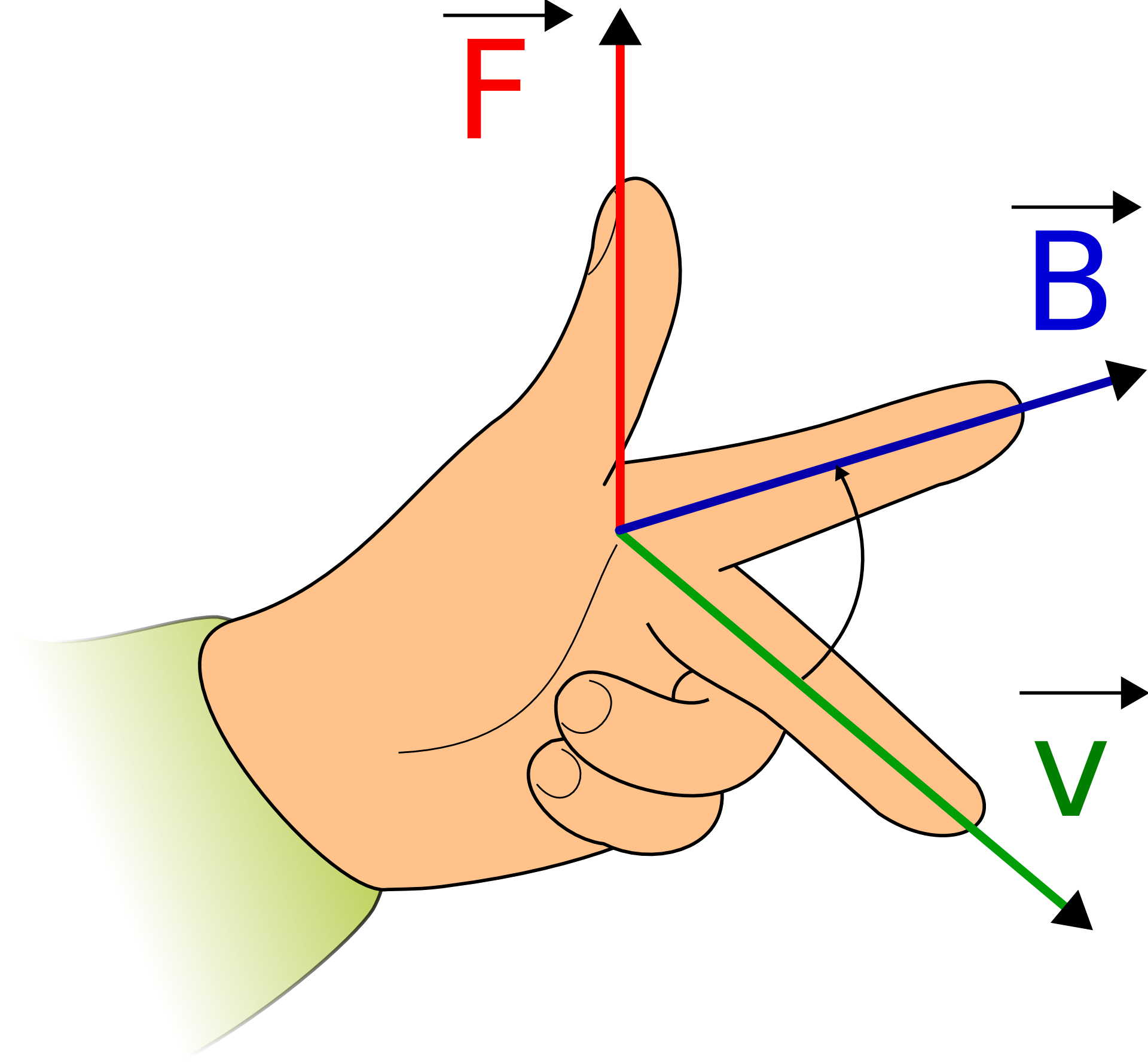
Odmiennym przypadkiem jest iloczyn wektorowy. Ma on sens jedynie w trójwymiarowym układzie współrzędnych. Długość tak wymnożonego wektora wyrazimy iloczynem długości wybranych wektorów i sinusa kąta między nimi. Ważne też jest, żeby odpowiednio dobrać ten kąt, tzn. wybrać mniejszy z nich. Wynika to z faktu, że rozpatrując większy kąt (konkretnie o mierze między 180 a 360 stopni), otrzymamy wynik ze znakiem minus. A jaki kierunek będzie miał nasz nowy wektor? Możemy posłużyć się tu regułą prawej dłoni. Na czym ona polega? Aby otrzymać prawidłowy wynik, musimy najpierw przesunąć wejściowe wektory tak, aby wychodziły z jednego miejsca. Oczywiście, nie zmieniamy przy tym ani ich kierunków ani zwrotów. Wektory stworzą wtedy pewną płaszczyznę.

Należy sobie wtedy wyobrazić linię, która jest do niej prostopadła i przechodzi przez punkt styku tych wektorów. Następnie należy otoczyć tę linię prawą dłonią tak, że kiedy ją zegniemy, to stworzymy łuk od wektora a do b, wokół mniejszego kąta między nimi. Wreszcie, kierunek kciuka wskaże nam zwrot wektora wyjściowego. A jak moglibyśmy to wyrazić algebraicznie? Wzór to opisujący jest skomplikowany, ale oszczędza nam wyobrażania sobie płaszczyzn i wygląda następująco: a x b = (aybz – byaz)*i + (azbx-bzax)*j+(axby-bxay)*k. Istnieje też iloczyn mieszany, korzystający z własności dwóch poprzednich, lecz jego obliczenie wymaga skomplikowanego aparatu matematycznego.

Przykłady wielkości wektorowych

Wiemy już, jak przekształcać wektory. Pozostaje nam jednak odpowiedź na pytanie, które wielkości wyrażamy w taki sposób? Przykładem jest wcześniej wspomniane przemieszczenie. Określa ono odległość w linii prostej od punktu początkowego do końcowego. Także prędkość i ściśle związane z nią przyspieszenie są wartościami wektorowymi. Ciekawostką jest, że prędkość ma odpowiadający sobie skalar – szybkość, który wyraża tylko jej wartość bezwzględną, nie biorąc pod uwagę jej kierunku czy zwrotu. Także siła jest wektorem. Również w matematyce mamy często do czynienia z wektorami, czy to na wczesnych etapach edukacji, rozpatrując kartezjański układ współrzędnych, a szczególnie na poziomie akademickim, na przykład rozpatrując liczby zespolone. Wszakże, możemy je zapisać jako wektor. Także dodawanie i mnożenie tych liczb podlega prawom obliczeń wektorowych. Ciekawostką jest, że ich wynalezienie pomogło znaleźć rozwiązanie dla wielu problemów nauk ścisłych, w tym także fizyki oraz techniki.

Wektory – jakie są zastosowania obliczeń na nich?

Być może zastanawiasz się teraz, dlaczego korzystamy z wektorów, skoro prawa działań na nich są tak odmienne? Odpowiedź na to pytanie jest bardzo prosta – upraszczają one znacząco zapis równań. Jedno proste równanie wektorowe (na przykład zsumowanie dwóch wektorów) zawiera w sobie trzy równania, nie mówiąc już o bardziej skomplikowanych przypadkach. Ponadto przy takim opisie tak naprawdę możemy wybrać dowolne, prostopadłe do siebie osie. Relacje między wektorami są także niezależne od położenia początku układu współrzędnych. Nic dziwnego, że wiele praw fizyki zapisujemy właśnie w takiej postaci. Niektóre wielkości wyrażamy też poprzez podobne twory, nazywane pseudowektorami. Dlaczego „tylko” pseudowektor? Wynika to z jego różnorodnego zachowania podczas transformacji. Gdy go obracamy, zachowuje się jak zwyczajny wektor, natomiast gdy mamy do czynienia z symetrią środkową, zmienia się na przykład tylko jego zwrot.

Pseudowektorami są zatem wszystkie twory, które mają swoje źródło w obrotach, na przykład prędkość kątowa czy moment pędu, a także te wektory związane z polem magnetycznym. Uogólnieniem tych wszystkich pojęć jest tensor, czyli tablica liczb, której własności są identyczne bez względu na to, jaki układ współrzędnych wybierzemy. Ma to swoje zalety – równania korzystające z tensorów, rozwiązane dla jednego układu współrzędnych, będzie prawdziwe dla każdego z nich. Umożliwia więc także rozważanie niestandardowych przestrzeni, np. krzywoliniowych czy ukośnokątnych. Oprócz wielkości wektorowych i pseudowektorowych, do tensorów należą także skalary i pseudoskalary, czyli iloczyny wielkości skalarnych i pseudowektorów.