5. Kinetyczna teoria gazów
Teoria kinetyczno-molekularna gazów wyjaśnia makroskopowe własności gazu na podstawie praw rządzących ruchem atomów, cząsteczek.
Podstawowy wzór teorii kinetycznej teorii gazów:
N – liczba molekuł gazu
V – objętość naczynia, w którym znajduje się gaz
![]() - średnia energia kinetyczna cząsteczek
- średnia energia kinetyczna cząsteczek
Średnia energia kinetyczna cząsteczek:
k – stała Boltzmanna
k = 1,38·10-23 J/K
T – temperatura gazu (podana w kelwinach)
Model gazu doskonałego:
- Gaz składa się z bardzo dużej liczby molekuł (rzędu mola), które znajdują się w nieustannym ruchu, zderzają się ze sobą wymieniając energię i pęd.
- Rozmiary molekuł są tak małe, że traktujemy je jak punkty materialne, to znaczy, że nie mają objętości
- Molekuły oddziałują ze sobą tylko w momentach zderzeń, a poza zderzeniami poruszają się ruchem jednostajnie prostoliniowym
- Zderzenia molekuł i molekuł ze ściankami naczynia są całkowicie sprężyste, to znaczy, że energia kinetyczna zostaje zachowana
- Jest dobrym przybliżeniem mocno rozrzedzonych gazów rzeczywistych
Równanie stanu gazu doskonałego dla stałej liczby molekuł:
p – ciśnienie gazu
V – objętość naczynia
T – temperatura gazu
Równanie Clapeyrona
pV = nRT
p – ciśnienie gazu
V – objętość naczynia
n – liczba moli
R – uniwersalna stała gazowa
T – temperatura gazu
k = R/NA
k – stała Boltzmanna
NA - liczba Avogadra
R - uniwersalna stała gazowa
R = 8,31 J/mol·K
Inny zapis równania Clapeyrona:
pV = NkT
Liczba stopni swobody – liczba niezależnych ruchów, jakie może wykonywać ciało; najmniejsza liczba współrzędnych, jakie potrzeba, aby opisać położenie ciała.
- Molekuła jednoatomowa – i = 3 (3 translacyjne stopnie swobody)
- Molekuła dwuatomowa – i = 5 (3 translacyjne i 2 rotacyjne stopnie swobody)
- Molekuła trójatomowa – i = 6 ( 3 translacyjne i 3 rotacyjne stopnie swobody)
Zasada ekwipartycji energii:
Na każdy stopień swobody molekuły przypada taka sama średnia energia kinetyczna równa ½ kT.
- 1 atom: i = 3,
- 2 atomy: i = 5,
- 3 atomy: i = 6,
Energia wewnętrzna gazu doskonałego – suma energii kinetycznej wszystkich molekuł
n – liczba moli
i – liczba stopni swobody
R – uniwersalna stała gazowa
T – temperatura gazu
Praca wykonana nad gazem
W = p·ΔV
W = nRΔT
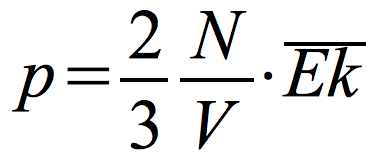

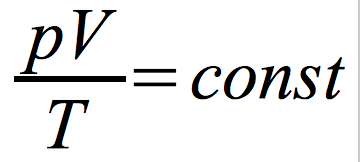
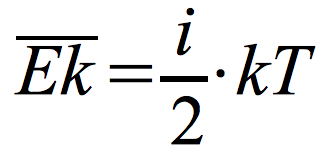
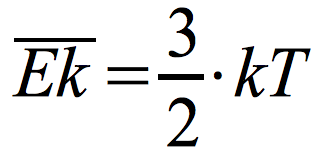
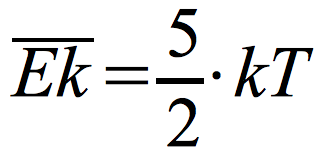

 (483 votes, average: 4,33 out of 5)
(483 votes, average: 4,33 out of 5)