4. Zwierciadła
Możliwe cechy obrazu:
- rzeczywisty / pozorny
- prosty / odwrócony
- równy / powiększony / pomniejszony
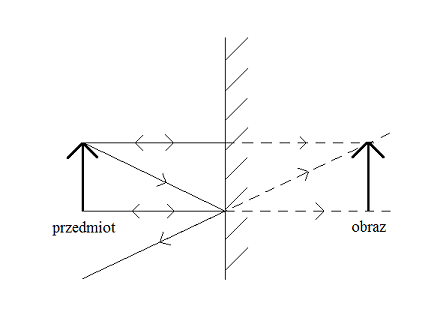
Zwierciadło płaskie
Cechy obrazu:
- pozorny – powstaje w wyniku przecięcia się przedłużeń promieni rzeczywistych
- prosty
- równy – tej samej wielkości
Powiększenie:
p > 1 – obraz powiększony
p < 1 – obraz pomniejszony
p = 1 – obraz równy
x – odległość przedmiotu od zwierciadła
y – odległość obrazu od zwierciadła
H – wysokość obrazu
h – wysokość przedmiotu
Zwierciadła kuliste
I. Zwierciadło wklęsłe
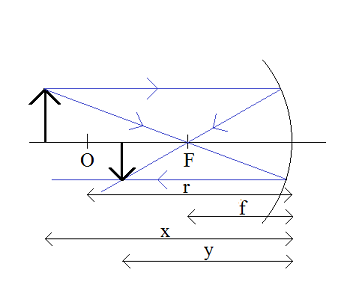
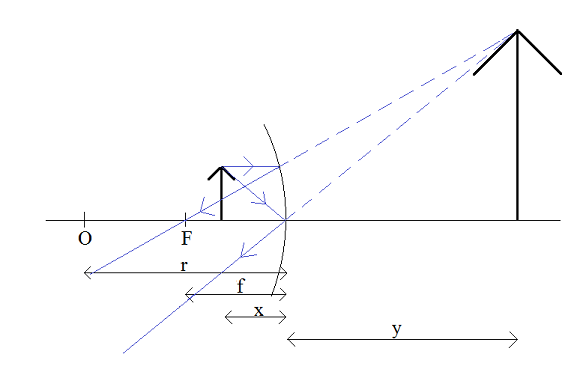
1. x > 2f
O – środek krzywizny zwierciadła
F – ognisko zwierciadła
r – promień krzywizny
f – ogniskowa zwierciadła
x – odległość przedmiotu od zwierciadła
y – odległość obrazu od zwierciadła
Otrzymany obraz:
- rzeczywisty
- odwrócony
- pomniejszony, y < x → p < 1
2. x = 2f
Otrzymany obraz:
- rzeczywisty
- odwrócony
- równy, y = x → p = 1
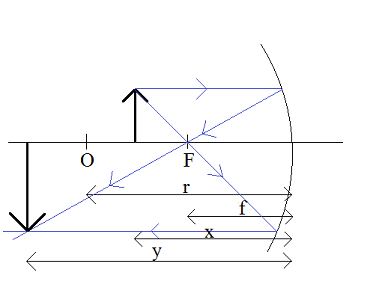
3. 2f < x < f
Otrzymany obraz:
- rzeczywisty
- odwrócony
- powiększony, y > x → p > 1
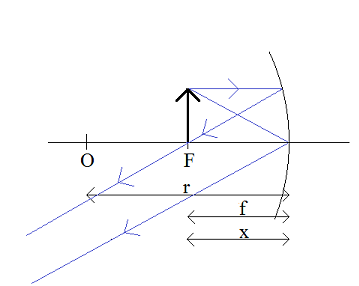
4. x = f
Obraz nie powstaje.
Promienie odbijają się i rozchodzą równolegle do siebie, nie krzyżując się w żadnym punkcie.
5. x < f
Otrzymany obraz:
- pozorny – powstał w przedłużenia promieni odbitych
- prosty
- powiększony, y > x → p > 1
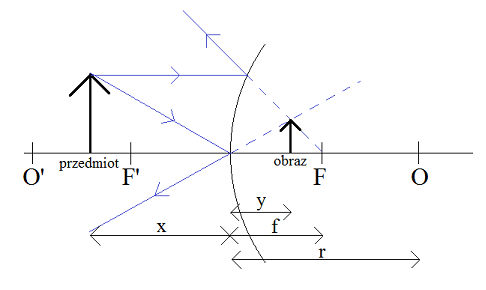
II. Zwierciadło wypukłe
Otrzymany obraz (dla każdego zwierciadła wypukłego):
- pozorny – powstał w przedłużenia promieni odbitych
- prosty
- pomniejszony, y < x → p < 1
Równanie zwierciadła kulistego:
f – ogniskowa zwierciadła
x – odległość przedmiotu od zwierciadła
y – odległość obrazu od zwierciadła
Przy czym dla obrazu pozornego odległość obrazu od zwierciadła y < 0 i otrzymujemy równanie
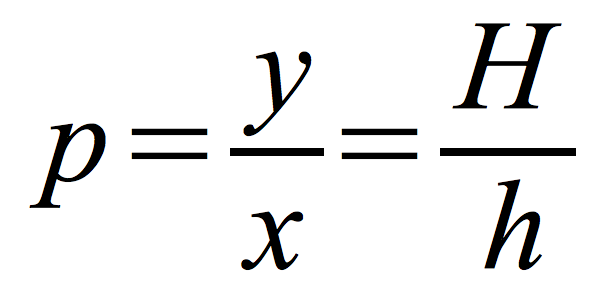

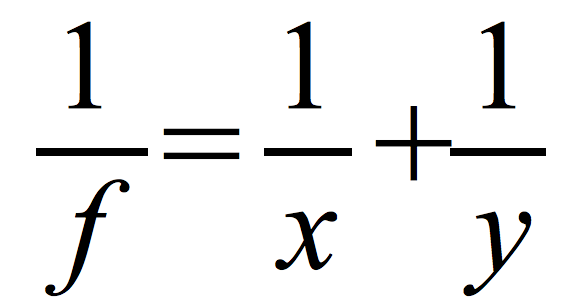
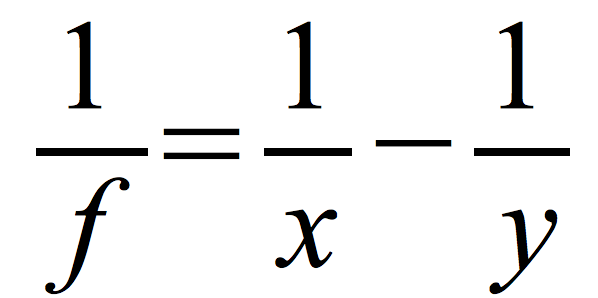

 (445 votes, average: 4,33 out of 5)
(445 votes, average: 4,33 out of 5)