3. Ruch harmoniczny
Siła harmoniczna – siła wprost proporcjonalna do wychylenia x z położenia równowagi, zwrócona w stronę odwrotną do wychylenia.
F = - k·x
k – współczynnik sprężystości
Oscylator harmoniczny – układ drgający, poddany działaniu siły harmonicznej
Amplituda xm – największe możliwe wychylenie z położenia równowagi
[ xm ] = 1m
Okres T – czas trwania jednego pełnego drgania
[T] = 1s
Częstotliwość f – liczba pełnych drgań w jednostce czasu
f = 1/T
[f] = 1/s = 1 Hz (herc)
Częstość kołowa
[ω ] = 1 Hz
Ruch oscylatora - wykresy
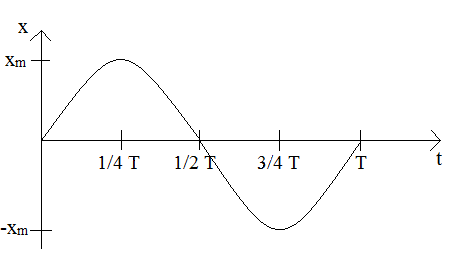
- położenie od czasu
x(t) = xm·sin(ωt + φ)
φ – faza początkowa
- prędkość od czasu
v(t) = xmω·cos(ωt + φ)
vmax = xmω
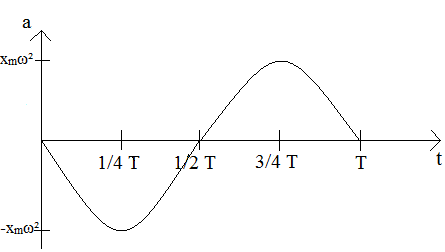
- przyspieszenie od czasu
a(t) = - xmω²·sin(ωt + φ)
amax = xmω²
Siła w ruchu harmonicznym
F = - xmω²·m·sin(ωt + φ)
Okres drgań harmonicznych
-kx = -ω²·m·x
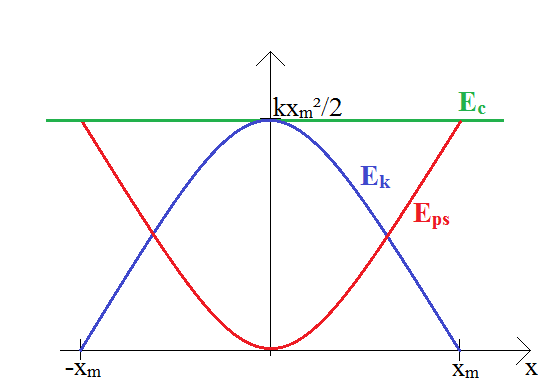
Energia w ruchu harmonicznym
Ek = mv²/2 = mxmω²·sin²(ωt)/2 = kxm²·cos²(ωt)/2
Eps = kx²/2 = kxm²·sin²(ωt)/2
Ec = Ek + Eps = kxm²/2·[sin²(ωt)+cos²(ωt)] = kxm²/2
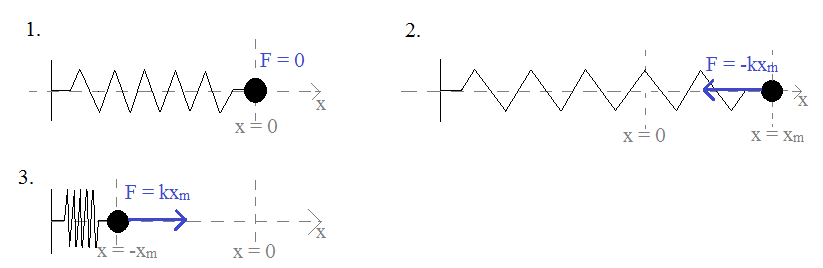
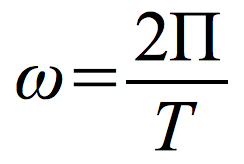

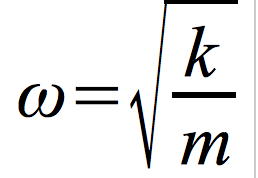
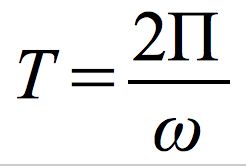
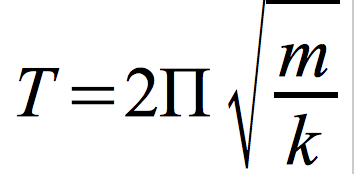

 (511 votes, average: 4,27 out of 5)
(511 votes, average: 4,27 out of 5)